para identificarlos por colores
sábado, 14 de septiembre de 2019
martes, 10 de septiembre de 2019
#10¿QUÉ ES EXCEL Y PARA QUÉ SIRVE?
Excel es un programa informático desarrollado por la empresa Microsoft y que forma parte de Office que es una suite ofimática que incluye otros programas como Word y PowerPoint.
¿PARA QUÉ SIRVE EXCEL?
Excel se distingue de todos los programas ofimáticos porque nos permite trabajar con datos numéricos. Con los números que almacenamos en Excel podremos realizar cálculos aritméticos básicos y también podremos aplicar funciones matemáticas de mayor complejidad, o utilizar funciones estadísticas.
Excel nos facilita en gran medida el trabajo con números y nos permite analizarlos fácilmente y generar reportes con herramientas como los gráficos y las tablas dinámicas.
EXCEL ES UNA HOJA DE CÁLCULO
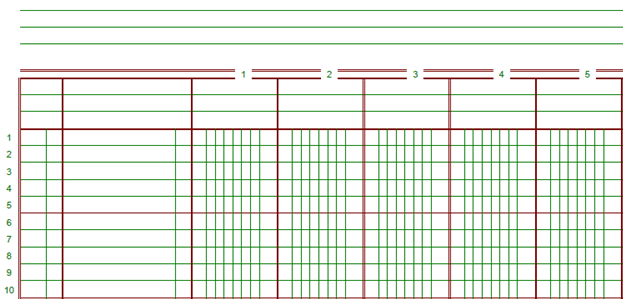
Excel pertenece a la categoría de programas informáticos conocida como hojas de cálculo. Las hojas de cálculo fueron desarrolladas desde la década de 1960 para simular las hojas de trabajo contables de papel y de esa manera ayudar en la automatización del trabajo contable.
Las hojas de cálculo electrónicas han ido reemplazando a los sistemas de cálculo en papel, y aunque inicialmente fueron creadas para tareas contables, hoy en día son utilizadas para un sinfín de aplicaciones donde se necesita trabajar con datos tabulares.
A PANTALLA PRINCIPAL DE EXCEL
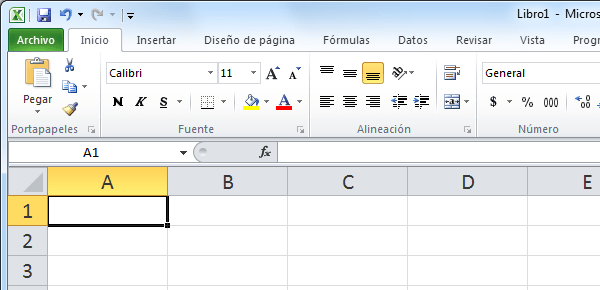
La característica principal de Excel, tal como lo conocemos hoy en día, es que la pantalla principal muestra una matriz de dos dimensiones, es decir, está formada por columnas y filas. De esta manera se forman pequeños recuadros que conocemos como celdas donde cada una de ellas tendrá una dirección única que estará conformada por la columna y la fila a la que pertenece, es decir, la dirección será una letra (columna) y un número (fila). Por ejemplo, la celda superior izquierda de la matriz tiene la dirección A1.
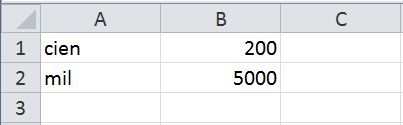
En cada una de las celdas podemos ingresar datos numéricos y alfanuméricos. Una manera de saber si Excel ha reconocido un dato como un número, o como un texto, es que si introducimos un dato de tipo texto se alineará a la izquierda de la celda mientras que los datos numéricos se alinearán a la derecha.
De esta manera sabemos que Excel reconoce entre un dato numérico y un dato alfanumérico en cada celda.
OPERACIONES ARITMÉTICAS EN EXCEL
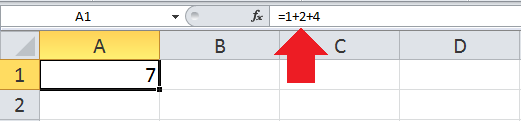
Excel nos permite realizar cálculos aritméticos con nuestros datos numéricos como la suma (+), la resta (-), la multiplicación (*) y la división (/). La única condición es que debemos colocar un signo igual (=) precediendo a la fórmula de manera que Excel efectúe el cálculo correspondiente.
Podemos escribir fórmulas tan grandes como lo necesitemos y solamente debemos respetar el máximo de caracteres que es de 32,767 en las versiones más recientes de Excel.
Algo que es extremadamente útil al momento de escribir fórmulas en Excel es que podemos hacer referencia a otras celdas para incluir sus valores dentro de los cálculos. A ese vínculo creado entre celdas lo conocemos como una referencia. Por ejemplo, la siguiente fórmula hará la suma de los valores en las celdas A1 y A2:
=A1+A2
Para conocer más sobre este tema te recomiendo leer el artículo: Referencias en Excel.
FUNCIONES DE EXCEL
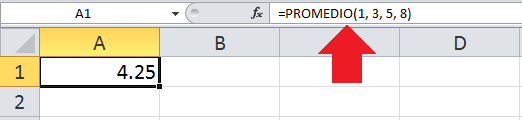
Aunque podemos utilizar los operadores aritméticos para realizar muchos de nuestros cálculos, podemos utilizar las funciones de Excel las cuales son procedimientos que nos ayudan a efectuar cálculos sobre nuestros datos. Podemos pensar en las funciones como si fueran un asistente de Excel al cual le daremos algunos datos numéricos y se encargarán de realizar los cálculos y entregarnos el resultado correcto.
Un ejemplo es la función PROMEDIO a quien podemos indicarle una serie de valores numéricos y nos devolverá el promedio de todos ellos.
Las funciones de Excel están catalogadas por su funcionalidad y algunas de esas categorías son las funciones de búsqueda y referencia, las funciones lógicas, las funciones de texto, las funciones de fecha y hora, etc.
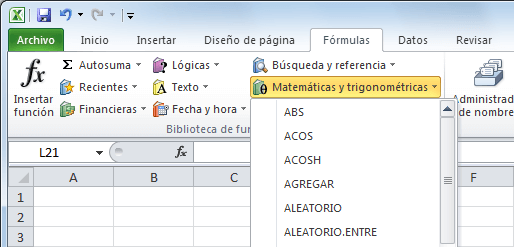
Para conocer todas las categorías de funciones disponibles en Excel puedes hacer clic sobre la pestaña Fórmulas y verás una serie de botones con los nombres de las categorías. Al hacer clic sobre cualquiera de ellos se mostrarán las funciones que pertenecen a dicha categoría, por ejemplo, la siguiente imagen muestra algunas de las funciones de la categoría Matemáticas y trigonométricas.
Otra alternativa para conocer las categorías y sus funciones es hacer clic en el menú Funciones de este sitio Web donde encontrarás el listado completo de funciones de Excel.
DATOS TABULARES EN EXCEL
Como lo he mencionado al principio, hoy en día Excel es utilizado en diversas disciplinas donde se necesiten datos tabulares. La gran cantidad de celdas, que forman cada una de las hojas de un libro de Excel, nos facilitan el organizar los datos de manera tabular.
Por esta razón Excel nos ofrece una buena cantidad de herramientas para dar formato a nuestros datos. Ya sea que necesitamos darles un formato de tabla de Excel, o que apliquemos un formato condicional o simplemente apliquemos algún estilo de celda.
Excel es una herramienta ampliamente utilizada para trabajar con datos tabulares ya que podremos ordenarlos, filtrarlos, hacer una búsqueda sobre ellos, o utilizar herramientas avanzadas para analizar dicha información.
GRÁFICOS EN EXCEL
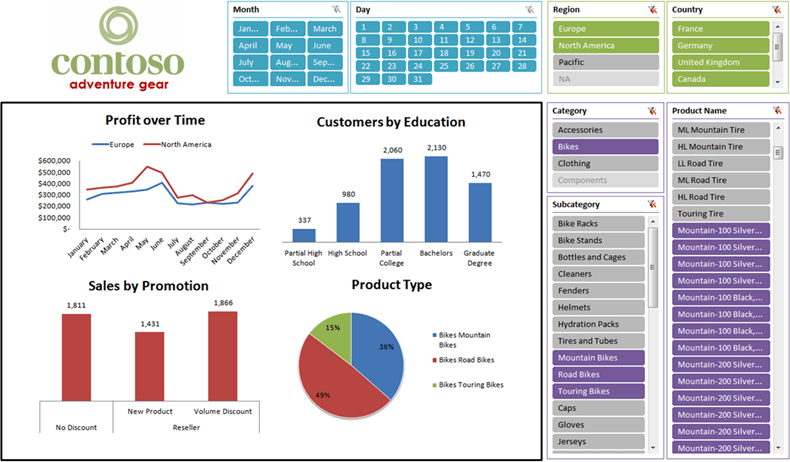
Una de las razones por las que Excel es una de las aplicaciones más populares alrededor del mundo es por su capacidad de crear gráficos basados en datos. El hecho de tener una herramienta visual facilita mucho la compresión e interpretación de la información por lo que millones de usuarios de la aplicación generan sus propios reportes en Excel.
Aprender a crear gráficos de Excel es un tema aparte, pero puedes tener una idea de los diferentes gráficos disponibles al hacer clic en la pestaña Insertar y de inmediato verás un grupo de comandos identificado con el nombre Gráficos donde podrás encontrar todos los tipos de gráficos disponibles en Excel.
lunes, 9 de septiembre de 2019
El software que ocupé para poder calcular las áreas, el perímetro, y las alturas fue "CALCMAPS"
Área IT : 187,441m2
Perímetro IT: 1,909m
Edificio mas alto: 9m
Edificio menos alto: 5m
Espacio deportivo:
Área: 27413 Metros2
Perímetro: 928 Metros
Biblioteca
Área:1302 Metros2
Perímetro:146 Metros
Perímetro:146 Metros
Altura:5 metros
Auditorio
Área:279 Metros2
Perímetro:70 Metros
Altura: 7metros
Croquis:
#7 Leyes de Murphy
"LEYES DE MURPHY"
1. 1Si algo puede salir mal, saldrá
mal.
2. Todo lleva más tiempo del que usted piensa.
3. Si existe la posibilidad de que varias cosas vayan mal, la que cause más perjuicios será la única que vaya mal.
4. Si usted intuye que hay cuatro posibilidades de que una gestión vaya mal y las evita, al momento aparecerá espontáneamente una quinta posibilidad.
5. Cuando las cosas se dejan a su aire, suelen ir de mal en peor.
6. En cuanto se ponga a hacer algo, se dará cuenta de que hay otra cosa que debería haber hecho antes.
7. Cualquier solución entraña nuevos problemas.
8. Es inútil hacer algo a prueba de tontos, porque los tontos son muy ingeniosos.
9. La naturaleza siempre está de parte de la imperfección oculta.
10. La madre naturaleza es una malvada.
11. Es imposible enseñar algo a alguien que cree saberlo.
12. Cuando se intente demostrar que algo no funciona, funcionará. (Esta ley es aplicable en viceversa)
13. No puedes ganar más de 3 veces seguidas. (a menos que trates de demostrarlo)
14. Si te despiertas de buen humor, siempre habrá algo que vuelva malo el día.
15. Cuando buscas algo, encontrarás todo lo perdido, menos lo buscado.
16. Cuando pares de buscar algo, lo encontrarás.
17. Si un artefacto no anda, apágalo y enciéndelo el día siguiente, volverá a funcionar como debe.
18. En la cocina, todos los objetos que caen, van a parar abajo de la alacena.
19. Cualquier objeto pequeño que caiga sobre un piso que tenga una rejilla, por más lejos que esté o más pequeña que sea, siempre va a parar a la rejilla.
20. En el patio siempre hay una silla rota.
21. Todo lo que parece que puede ser beneficioso resulta una ruina.
22. Si explicas algo de modo que lo puedan entender los alumnos, el profesor no lo entenderá.
23. Si se te pierde algo en la calle, por mucho que busques no lo encontrarás.
24. Cada reparación crea nuevas averías.
25. Si tienes papel, no tendrás bolígrafo, si tienes bolígrafo, no tendrás papel; y si tienes papel y bolígrafo, no necesitarás escribir nada.
26. Si tienes algo importante que decirle a una persona, no la encontrarás; si la encuentras, olvidarás lo que tienes que decirle; si lo recuerdas, la persona ya se habrá ido
27. Si está pendiente de que no se derrame la leche al hervirla, lo más seguro es que en el preciso momento en que se distraiga un segundo se derrama.
28. Cuando tienes una pertenencia que no se usa o no se necesita, y a futuro te deshaces de ella, la vas a necesitar urgentemente.
29. Si en una prueba de Matemáticas entre 10.000 temas hay uno del que no estas seguro, ten claro que de eso se va a tratar la prueba
30. Todo aquello que no es una afirmación, debe considerarse una negación.
2. Todo lleva más tiempo del que usted piensa.
3. Si existe la posibilidad de que varias cosas vayan mal, la que cause más perjuicios será la única que vaya mal.
4. Si usted intuye que hay cuatro posibilidades de que una gestión vaya mal y las evita, al momento aparecerá espontáneamente una quinta posibilidad.
5. Cuando las cosas se dejan a su aire, suelen ir de mal en peor.
6. En cuanto se ponga a hacer algo, se dará cuenta de que hay otra cosa que debería haber hecho antes.
7. Cualquier solución entraña nuevos problemas.
8. Es inútil hacer algo a prueba de tontos, porque los tontos son muy ingeniosos.
9. La naturaleza siempre está de parte de la imperfección oculta.
10. La madre naturaleza es una malvada.
11. Es imposible enseñar algo a alguien que cree saberlo.
12. Cuando se intente demostrar que algo no funciona, funcionará. (Esta ley es aplicable en viceversa)
13. No puedes ganar más de 3 veces seguidas. (a menos que trates de demostrarlo)
14. Si te despiertas de buen humor, siempre habrá algo que vuelva malo el día.
15. Cuando buscas algo, encontrarás todo lo perdido, menos lo buscado.
16. Cuando pares de buscar algo, lo encontrarás.
17. Si un artefacto no anda, apágalo y enciéndelo el día siguiente, volverá a funcionar como debe.
18. En la cocina, todos los objetos que caen, van a parar abajo de la alacena.
19. Cualquier objeto pequeño que caiga sobre un piso que tenga una rejilla, por más lejos que esté o más pequeña que sea, siempre va a parar a la rejilla.
20. En el patio siempre hay una silla rota.
21. Todo lo que parece que puede ser beneficioso resulta una ruina.
22. Si explicas algo de modo que lo puedan entender los alumnos, el profesor no lo entenderá.
23. Si se te pierde algo en la calle, por mucho que busques no lo encontrarás.
24. Cada reparación crea nuevas averías.
25. Si tienes papel, no tendrás bolígrafo, si tienes bolígrafo, no tendrás papel; y si tienes papel y bolígrafo, no necesitarás escribir nada.
26. Si tienes algo importante que decirle a una persona, no la encontrarás; si la encuentras, olvidarás lo que tienes que decirle; si lo recuerdas, la persona ya se habrá ido
27. Si está pendiente de que no se derrame la leche al hervirla, lo más seguro es que en el preciso momento en que se distraiga un segundo se derrama.
28. Cuando tienes una pertenencia que no se usa o no se necesita, y a futuro te deshaces de ella, la vas a necesitar urgentemente.
29. Si en una prueba de Matemáticas entre 10.000 temas hay uno del que no estas seguro, ten claro que de eso se va a tratar la prueba
30. Todo aquello que no es una afirmación, debe considerarse una negación.
#6 Teorema de la computación
Teoremas sobre las máquinas de Turing
Lenguaje Recursivamente Enumerable
Recordemos que llamamos
lenguaje Recursivamente Enumerable (RE) a los
lenguajes que pueden ser aceptados por una Máquina de Turing.
Teorema
1
Todo lenguaje aceptado por una
Máquina de Turing de varias cintas es Recursivamente Enumerable.
Teorema
2
Sea L = L(M) el
lenguaje que acepta una máquina de Turing no determinista M,
entonces existe una máquina de Turing deterministaN que acepta
dicho lenguaje, es decir, L(M) =L (N).
Lenguajes de máquinas de Turing y de Autómatas
Teorema
3
Sea L el
lenguaje aceptado por una máquina de Turing, entonces existe algún Autómata de
dos pilas que acepta L.
Teorema
4
Todo lenguaje Recursivamente
Enumerable es aceptado por alguna máquina de tres contadores.
Teorema
5
Todo lenguaje Recursivamente
Enumerable es aceptado por alguna máquina de dos contadores.
#5 Sistema operativo
Un sistema
operativo es el software o programa más importante que se
ejecuta en un computador, nos permite usarlo y darle órdenes para que haga lo
que necesitamos.
Son
importantes, porque te permiten interactuar y darle órdenes al computador. Sin
un sistema operativo el computador es inútil.
Sin el
sistema operativo, no tendrías la plataforma que soporta los programas que te
permiten hacer cartas, escuchar música, navegar por internet o enviar un
correo electrónico.
Administra
los recursos del computador, es decir, el software y hardware de tu
equipo. Es la estructura que soporta y maneja todos los programas y partes de
tu computador.
CLASIFICACIÓN
CLASIFICACIÓN
Sistemas operativos monousuarios
Los sistemas operativos monousuarios son aquellos que soportan a un usuario a la vez, sin importar el número de procesadores que tenga la computadora o el número de procesos o tareas que el usuario pueda ejecutar en un mismo instante de tiempo. Las computadoras personales típicamente se han clasificado en este renglón.
Sistemas operativos multiusuarios
Los sistemas operativos multiusuarios son capaces de dar servicio a más de un usuario a la vez, ya sea por medio de varias terminales conectadas a la computadora o por medio de sesiones remotas en una red de comunicaciones. No importa el número de procesadores en la máquina ni el número de procesos que cada usuario puede ejecutar simultáneamente.
Sistemas operativos monotareas
Los sistemas monotarea son aquellos que sólo permiten una tarea a la vez por usuario. Puede darse el caso de un sistema multiusuario y monotarea, en el cual se admiten varios usuarios al mismo tiempo pero cada uno de ellos puede estar haciendo solo una tarea a la vez.
Sistemas operativos multitareas
Un sistema operativo multitarea es aquél que le permite al usuario estar realizando varias labores al mismo tiempo. Por ejemplo, puede estar editando el código fuente de un programa durante su depuración mientras compila otro programa, a la vez que está recibiendo correo electrónico. Es común encontrar en ellos interfaces gráficas orientadas al uso de menús y el ratón, lo cual permite un rápido intercambio entre las tareas para el usuario, mejorando su productividad.
Sistemas operativos uniproceso
Un sistema operativo uniproceso es aquél capaz de manejar solamente un procesador de la computadora, de manera que si la computadora tuviese más de uno le sería inútil. El ejemplo más típico de este tipo de sistemas es el DOS y MacOS.
Sistemas operativos multiproceso
Un sistema operativo multiproceso se refiere al número de procesadores del sistema, que es más de uno y éste es capaz de usarlos todos para distribuir su carga de trabajo. Generalmente estos sistemas trabajan de dos formas: simétrica o asimétricamente. Cuando se trabaja de manera asimétrica, el sistema operativo selecciona a uno de los procesadores el cual jugará el papel de procesador maestro y servirá como pivote para distribuir la carga a los demás procesadores, que reciben el nombre de esclavos. Cuando se trabaja de manera simétrica, los procesos o partes de ellos son enviados indistintamente a cualquiera de los procesadores disponibles, teniendo, teóricamente, una mejor distribución y equilibrio en la carga de trabajo bajo este esquema.
Suscribirse a:
Entradas (Atom)